- Yazar Jason Gerald [email protected].
- Public 2024-01-16 20:04.
- Son düzenleme 2025-01-23 12:50.
Hız, bir şeyin bir anda ne kadar hızlı hareket ettiğinin hesaplanmasıdır. Hareket halindeki bir arabanın hız göstergesine daha önce baktıysanız, hız sayısını görürsünüz - ibre ne kadar uzağa giderse, aracın hızı da o kadar yüksek olur. Sahip olduğunuz bilgi türüne bağlı olarak hızı hesaplamanın birkaç yolu vardır. Genel olarak, formül hız = mesafe/zaman (veya k = j/w) hızı hesaplamanın en kolay yoludur.
Adım
Yöntem 1/3: Standart Hız Hesaplama Formüllerini Kullanma

Adım 1. Bir nesnenin kat ettiği mesafeyi bulun
Çoğu insanın bir şeyin hızını bulmak için kullandığı temel formülün kullanımı çok kolaydır. Her şeyden önce, “ölçülen nesnenin ne kadar mesafe kat ettiğini” bilmeniz gerekir. Başka bir deyişle, nesnenin başlangıç noktası ile bitiş noktası arasındaki mesafe nedir?
Bu formülü bir örnekle anlamak daha kolaydır. Diyelim ki araba ile "161 kilometre" bir oyun alanına gidiyoruz. Birkaç adımda, formülün hesaplamasını tamamlamak için bu bilgileri kullanabiliriz

Adım 2. Cismin bu mesafeyi kat etmesi için geçen süreyi bulun
İhtiyacınız olan bir sonraki bilgi, nesnenin belirli bir mesafeye ulaşmasının ne kadar sürdüğüdür. Başka bir deyişle, nesnenin başlangıç noktasından bitiş noktasına hareket etmesi ne kadar sürer?
Bu örnekte, nesnenin yakl. iki saat hedefe ulaşmak için.

Adım 3. Cismin hızını bulmak için mesafeyi geçen zamana bölün
Nesnenin hızını bilmek için sadece bu iki bilgiye ihtiyacınız var. Zamana olan mesafe cismin hızına eşittir.
Bu örnekte, 161 kilometre/2 saat = 80,5 kilometre/saat.

Adım 4. Kullanılan birimi unutmayın
Cevabınızda doğru birimleri kullanmanız çok önemlidir (saatte kilometre vb.) Bu birimler olmadan, insanların cevabınızın anlamını anlaması çok zordur. Okuldan ödevler yaparken yanlış üniteyi kullanırsanız da puan kaybedebilirsiniz.
Hızın birimi zaman birimine uzaklık birimi. Örneğin, mesafeyi kilometre ve zamanı saat cinsinden ölçtüğümüz için kullanılan birimler şunlardır: kilometre/saat (veya saatte kilometre).
Yöntem 2/3: Daha Zor Hesaplamaları Çözme

Adım 1. Mesafe ve zaman problemini çözmek için birkaç farklı değişken bulun
Hızın temel formülünü anladıktan sonra, bunu hız dışındaki hesaplamaları yapmak için kullanabilirsiniz. Örneğin, ilk başta yalnızca nesnenin hızını ve diğer bir değişkeni biliyorsanız, bilinmeyen bilgileri bulmak için yukarıdaki formülü yeniden düzenleyebilirsiniz.
-
Örneğin, bir trenin dört saat boyunca saatte 20 kilometre hızla gittiğini bildiğimizi, ancak ne kadar yol kat ettiğini bilmediğimizi varsayalım. Bunu bulmak için formülü aşağıdaki şekilde yeniden düzenleyebiliriz:
-
- hız = mesafe/zaman
- hız × zaman = (mesafe/zaman) × zaman
- hız × zaman = mesafe
- 20 km/saat × 4 saat = mesafe = 80 kilometre
-

Adım 2. Kullandığınız birimleri gerektiği gibi dönüştürün
Bazen belirli bir birimi kullanarak hızı hesaplayabilirsiniz, ancak bunu başka bir birime dönüştürmeniz gerekir. Bu durumda doğru birimlere göre cevap alabilmek için bir dönüştürme faktörü kullanmanız gerekir. Bunu yapmak için, birimler arasındaki ilişkiyi kesir biçiminde yazmanız ve çarpmanız yeterlidir. Çarparken, istenmeyen birimleri çıkarmak için kesri gerektiği gibi ters çevirin. Bu yöntem göründüğünden çok daha kolay!
-
Örneğin yukarıdaki örnek problemde cevaba kilometre yerine mil olarak ihtiyacımız olduğunu söyleyelim. Bir mil yaklaşık 1,6 kilometreye eşittir. Buna göre dönüşümü şu şekilde yapabiliriz:
-
- 80 kilometre × 1 mil/1,6 kilometre = 50 mil
-
- Unutmayın, kilometreler kesrin alt kısmında göründüğü için önceki yanıttan kilometreleri çıkarır, bu nedenle nihai sonuç mil kullanır.
- Bu web sitesi, yaygın olarak kullanılan birimlerin çoğu için dönüştürme özellikleri sağlar.

Adım 3. "Mesafe" değişkenini gerektiği gibi mesafe formülüyle değiştirin
Nesneler her zaman düz, pürüzsüz bir yolda hareket etmezler. Bu doğruysa, standart hız formülüne uzaklık birimi olarak basitçe sayısal bir değer giremeyebilirsiniz. Ancak, k = j/w formülündeki j harfini, nesnenin kat ettiği mesafeye benzeyen bir formülle değiştirmeniz gerekebilir.
-
Örneğin, bir uçağın havada 20 mil 5 kez döndüğünü varsayalım. Uçak turu yarım saatte tamamladı. Bu örnekte, hızını belirlemeden önce uçağın kat ettiği toplam mesafeyi bulmamız gerekiyor. Bir dairenin etrafındaki mesafeyi (çevresindeki mesafeyi) hesaplamak için bu formülde j yerine formülü kullanabiliriz. Bu formül çevre = 2πr'dir, burada r = dairenin yarıçapı. Bunu nasıl çözeceğiniz aşağıda açıklanmıştır:
-
- k = (2 × × r)/w
- k = (2 × 10)/0.5
- k = 62.83/0.5 = 125.66 mil/saat
-

Adım 4. k = j/w'nin ortalama hızı verdiğini anlayın
Hızı bulmak için kullandığımız kolay ve basit formülün bir dezavantajı var. Ortaya çıkan değer teknik olarak ortalama hızdır. Bu, formülün ölçtüğünüz nesnenin hareket ederken aynı hızı kullandığını varsaydığı anlamına gelir. Aşağıda göreceğimiz gibi, bir cismin hızını tek bir anda bulmak çok daha zor olacaktır.
Bu farkı göstermek için, en son ne zaman arabayla seyahat ettiğinizi hayal edin. Seyahat ettiğiniz hızda seyahat etmeniz pek olası değildir. Ancak, yolculuğunuza genellikle düşük bir hızda başlayacak ve yol boyunca hızınızı kademeli olarak artıracak, kırmızı ışıklar, trafik sıkışıklığı vb. Yolculuk sırasında hızı bulmak için standart hız formülünü kullanırsanız, bu hızdaki değişiklikler algılanamaz. Ancak, seyahat ettiğiniz tüm hız farklarının ortalama hızını gösteren bir yanıt alacaksınız
Yöntem 3/3: Anlık Hızı Hesaplama
Not:
Bu bölüm, hiç kalkülüs eğitimi almamış kişilere daha az aşina olan teknikleri kullanır. Yardım için matematiğe ilişkin makalelerimizi okuyun.
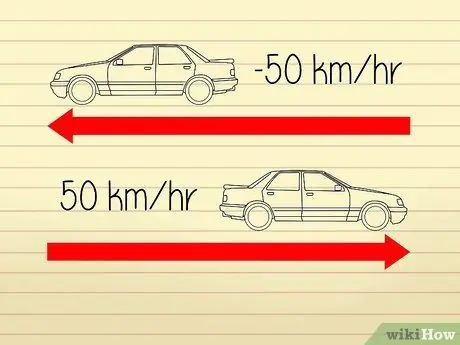
Adım 1. Hızın ivme oranı olarak tanımlandığını anlayın
Yüksek seviyeli hız hesaplamaları oldukça kafa karıştırıcıdır çünkü matematikçiler ve bilim adamları "hız" ve "ivme"yi tanımlamak için farklı tanımlar kullanırlar. Hızlanmanın iki bileşeni vardır: "hız" ve "yön". Hız, nesnenin hızına eşittir. Yöndeki bir değişiklik, ivmede bir değişikliğe neden olur, ancak hızda bir değişikliğe neden olmaz.
- Örneğin, iki arabanın zıt yönlerde hareket ettiğini varsayalım. Her iki arabadaki hızölçerler de 50 km/s'lik bir rakam gösteriyor, bu yüzden ikisi de aynı hızda seyahat ediyor. Ancak arabalar birbirinden uzaklaştığından, arabalardan birinin -50 km/h “hızlanması”, diğerinin ise 50 km/h “hızlanması” olduğunu söyleyebiliriz.
- Anlık hız hesaplamaları gibi anlık hızlanma hesaplamaları da yapabilirsiniz.

Adım 2. Negatif ivmeyi ölçmek için mutlak değerleri kullanın
Bir nesne negatif bir hızlanma oranına sahip olabilir (eğer başka bir nesneye göre negatif yönde hareket ediyorsa). Ancak, olumsuz bir hız yoktur. Bu durumda, oranın mutlak değeri cismin hızını gösterir.
Bu nedenle yukarıdaki örnek problemde her iki arabanın da hızı 50km/s.
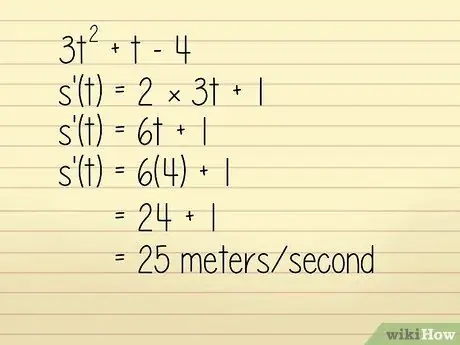
Adım 3. Fonksiyonun konumunun türevini alın
Eğer bir cismin konumunu zamanı hesaplamadan gösteren bir k(w) fonksiyonunuz varsa, k(w)'nin türevi zamanlamaya gerek duymadan ivmeyi gösterecektir. Sadece zaman değerini bu formüle ekleyin, böylece w değişkeni (veya hangi zaman değeri kullanılıyorsa) o zamana göre hızlanır. Buradan cismin hızını kolayca bulabilirsiniz.
-
Örneğin, bir cismin bir metredeki konumunun 3q denkleminde tanımlandığını varsayalım.2 + w - 4 burada w = saniye cinsinden süre. Cismin w = 4 saniyedeki hızını bilmek istiyoruz. Bu durumda, bunu şu şekilde çözebilirsiniz:
-
- 3w2 +w - 4
- k'(w) = 2 × 3w + 1
- k'(w) = 6w + 1
-
-
Şimdi w = 4 giriyoruz:
-
- k'(w) = 6(4) + 1 = 24 + 1 = 25 metre/saniye. Teknik olarak bu bir ivme hesabıdır, ancak pozitif olduğu ve soruda yönden bahsedilmediği için hızı bulmak için kullanabiliriz.
-

Adım 4. İntegral ivme fonksiyonunu alın
Hızlanma, bir cismin zaman içindeki ivmesindeki değişimi ölçmenin bir yoludur. Bu konu, bu makalede tam olarak açıklanamayacak kadar karmaşıktır. Bununla birlikte, zamana göre ivmeyi temsil eden bir a(w) fonksiyonuna sahip olduğunuzda, a(w)'nin integralinin o zamana dayalı ivme sonucunu döndüreceğini not etmek faydalı olacaktır. Unutmayın, bir nesnenin ilk ivmesini bilmek çok faydalıdır, böylece sonsuz bir integralden o sonucun sabitini tanımlayabilirsiniz.
-
Örneğin, bir nesnenin sabit bir ivmeye sahip olduğunu varsayalım (m/s olarak2 a(w) = -30'un bir sonucu olarak. Ayrıca cismin başlangıç ivmesinin 10 m/s olduğunu söyleyin. w = 12 saniyedeki hızı bulmamız gerekiyor. Bu durumda şu şekilde çözebiliriz:
-
- a(w) = -30
- p(w)= a(w)dw = -30dw = -30w + C
-
-
C'yi bulmak için w = 0 için p(w)'yi çözeceğiz. Cismin ilk ivmesinin 10 m/s olduğunu unutmayın.
-
- p(0) = 10 = -30(0) + C
- 10 = C, yani p(w) = -30w + 10
-
-
Artık w = 12 saniye girebiliriz.
-
- p(12) = -30(12) + 10 = -360 + 10 = -350. Hız, ivmenin mutlak bir değeri olduğundan, cismin hızı 350 metre/saniye.
-
İpuçları
- Pratik yapmak harikadır! Yukarıdaki örnek problemdeki sayıları değiştirerek kendi sorunuzu oluşturmaya çalışın.
- Daha iyi hesaplama hızı için kalkülüs alıştırması yapmanın hızlı bir yolunu arıyorsanız, buradaki çevrimiçi türev hesaplayıcıyı ve buradaki çevrimiçi integral hesaplayıcıyı kullanın.






