- Yazar Jason Gerald [email protected].
- Public 2024-01-15 08:25.
- Son düzenleme 2025-01-23 12:50.
Bölmeyi yapmanın çeşitli yolları vardır. Ondalık sayıları, kesirleri ve hatta üsleri bölebilir ve uzun veya kısa bölmeyi kullanabilirsiniz. Sayıları bölmenin farklı yollarını bilmek istiyorsanız, aşağıdaki adımları izleyin.
Adım
Yöntem 1/5: Uzun Seri Bölümünü Gerçekleştirme

Adım 1. Soruları yazın
Uzun bölme yapmak için paydayı (bölünecek sayıyı) bölen çubuğunun dışına, payı (bölünecek sayıyı) bölen çubuğunun içine yerleştirin.
Örneğin: 136÷3

Adım 2. Payın ilk basamağını paydaya bölün (mümkünse)
Bu örnekte 1, 3'e bölünemez, bu nedenle bölen çubuğun üzerine 0 koyun ve bir sonraki adıma geçin. 1 ile 0 çıkarın ve sonucu 1 sayısının altına koyun.

Adım 3. Payın ilk basamağının kalanını ve payın ikinci basamağını paydaya bölün
1 sayısı 3'e bölünemediği için 1 sayısı hala kullanılmaktadır. 3'ü çıkarmanız gerekiyor. Şimdi 13'ü 3'e bölün. 3 x 4 = 12 olduğundan, 4'ü bölen çubuğun üstüne (0'ın sağına) koyun, ardından 13'ü 12'den çıkarın ve sonucu altına yazın.

Adım 4. Kalan sayıları paydaya bölün
6 sayısını 1'in sağına düşürün, 16 elde edin. Şimdi 16'yı 3'e bölün. 3 x 5 = 15 olduğuna göre, 5 sayısını 4'ün sağına yazın ve 16'yı 15'e çıkarın ve sonucu yazın (16-15= 1) altında.

Adım 5. Kalanı bölümün yanına yazın
Son cevabınız 1 kalan 45 veya 45 R1'dir.
Yöntem 2/5: Kısa Bölmeleri Gerçekleştirme

Adım 1. Soruları yazın
Bölen çubuğun dışına paydayı (bölünecek sayı) ve bölen çubuğunun içine payı (bölünecek sayı) yazın. Kısa bölmede paydanın birden fazla basamak olamayacağına dikkat edin.
Örneğin, 518 4

Adım 2. Payın ilk basamağını paydaya bölün
5 4 = 1 R1. Bölümü (1) uzun ayırıcı çubuğun üzerine yerleştirin. Kalanı payın ilk basamağının üstüne yazın. 5'i 4'e böldüğünüzde 1 kaldığını hatırlatmak için küçük bir 1 bölü 5 yerleştirin. 518 şimdi şöyle görünmelidir: 5118

Adım 3. Kalandan ve payın ikinci basamağından oluşan sayıyı paydaya bölün
Bir sonraki sayı, artık değer (1) ve payın (1) ikinci hanesinden elde edilen 11'dir. 11 4 = 2 R 3 çünkü 4 x 2 = 8 kalan 3'tür. Kalan değeri payın ikinci basamağının üzerine yazın. 3 bölü 1 koyun. İlk pay (518) şimdi şöyle görünür: 51138

Adım 4. Kalan sayıları paydaya bölün
Kalan sayı 38'dir; 3 sayısı önceki aşamanın geri kalanından gelir ve 8, payın son basamağıdır. 38 4 = 9 R2 hesaplayın. 4 x 9 = 36 olduğundan bölme çubuğunun üstüne "R2" yazın çünkü 38 - 36 = 2.

Adım 5. Son cevabı yazın
Nihai sonuç ve bölüm, bölen çubuğunun üzerindedir. Cevap 518 4 = 129 R2'dir.
Yöntem 3/5: Kesirleri Böl

Adım 1. Soruları yazın
Bir kesri bölmek için, ilk kesri, ardından bölme sembolünü ve ardından ikinci kesri yazmanız yeterlidir.
Örneğin: 3/4 5/8

Adım 2. İkinci kesrin payını ve paydasını ters çevirin
İkinci kesir artık karşılıklıdır.
Örnek: 3/4 8/5

Adım 3. Bölme sembolünü çarpı sembolüyle değiştirin
Bir kesri bölmek için ilk kesri ikincinin tersiyle çarparsınız.
Örnek: 3/4 x 8/5
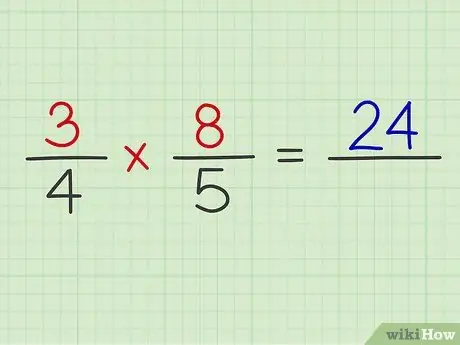
Adım 4. Her iki kesrin payını çarpın
Sadece iki normal kesri çarpıyormuş gibi yapın.
Örnek: 3 x 8 = 24
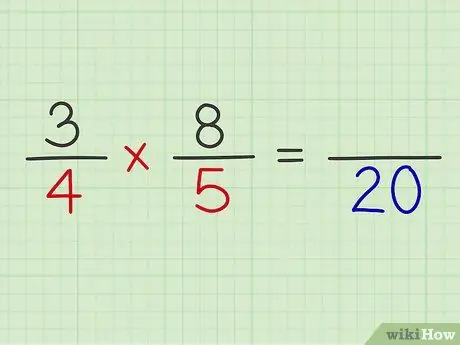
Adım 5. Her iki kesrin paydalarını çarpın
İki kesri çarparak hesaplamayı tamamlayın.
Örnek: 4 x 5 = 20
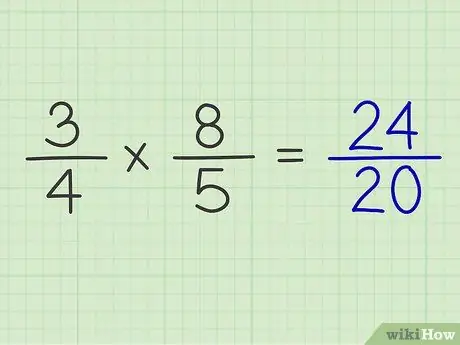
Adım 6. Payın çarpımını paydanın çarpımının üzerine koyun
İki kesrin payını ve paydasını çarptıktan sonra, her iki kesrin de hesaplanmasının sonucunu elde edebilirsiniz.
Örnek: 3/4 x 8/5 = 24/20

Adım 7. Kesirleri basitleştirin
En Büyük Ortak Çarpanı veya payı ve paydayı eşit olarak bölen en büyük sayıyı bulmak için. Bu durumda 24 ve 20'nin en büyük ortak çarpanı 4'tür. Bunu ispatlamak için tüm pay ve paydaları yazın ve her ikisinin en büyük ortak çarpanlarının sayısını daire içine alın.
- 24: 1, 2, 3, 4, 6, 8, 12, 24
-
20: 1, 2, 4, 5, 10, 20
- 4, 24 ve 20'nin en büyük ortak çarpanı olduğundan, kesri sadeleştirmek için iki sayıyı 4'e bölmeniz yeterlidir.
- 24/4 = 6
- 20/4 = 5
- 24/20 = 6/5

Adım 8. Kesri karışık sayı olarak yeniden yazın (isteğe bağlı)
İşin püf noktası, sadece payı paydaya bölün ve sonucu tam sayı olarak yazın. Bundan sonra bölmenin kalanını yeni bir pay olarak yazın ve kesrin paydası değişmez. 6'nın 5'e bölünmesi, 1 kalanını 1 olarak verdiğinden, 1 tam sayısını, ardından yeni pay 1'i, ardından payda 5'i karışık bir 1 1/5 sayısı elde etmek için yazın.
Örnek: 6/5 = 1 1/5
Yöntem 4/5: Üs Böl

Adım 1. Üslerin/kuvvetlerin aynı taban numarasına sahip olduğundan emin olun
Üsleri yalnızca aynı taban numaralarına sahiplerse bölebilirsiniz. Aksi takdirde, aynı temel sayıyı elde edene kadar bunları değiştirmeyi deneyebilirsiniz.
Örnek: x8 x5

Adım 2. Üslü çıkarın
Sadece ilk üssü ikinciden çıkarabilirsiniz. Şimdilik baz sayıları önemsemeyin.
Örnek: 8 - 5 = 3
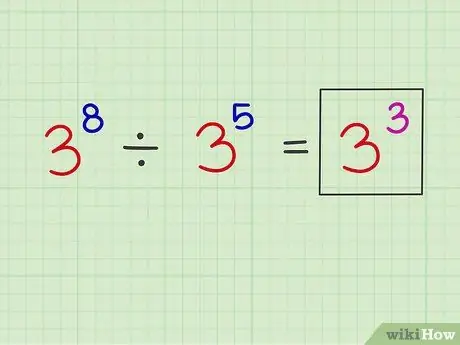
Adım 3. Yeni üssü orijinal taban numarasının üzerine yerleştirin
Şimdi, yeni üssü orijinal taban numarasının üzerine yazabilirsiniz.
Örnek: x8 x5 = x3
Yöntem 5/5: Ondalık Sayıları Bölme

Adım 1. Soruları yazın
Bölen çubuğun dışına paydayı (bölünecek sayı) ve bölen çubuğun içine payı (bölünecek sayı) yazın. Ondalık bölmede amacınız ondalık bir sayıyı tam sayıya dönüştürmektir.
Örnek: 65.5.5

Adım 2. Paydayı tam sayı olarak değiştirin
0,5'ten 5'e, yani 5, 0'a değiştirmek için ondalık noktayı bir basamak sağa kaydırmanız yeterlidir.

Adım 3. Ondalık noktayı payda ile aynı sayıda basamak kaydırarak payı değiştirin
Payın ondalık noktasını tam sayı olacak şekilde bir basamak sağa hareket ettirdiğiniz için, paydanın ondalık noktası da bir basamak sağa kaydırılır, böylece 65.5 655 olur.
Payın ondalık noktasını tüm basamaklarının ötesine kaydırırsanız, ondalık nokta her kaydırıldığında basamaklara sıfır eklemeniz gerektiği anlamına gelir. Örneğin, 7, 2 ondalık noktası üç basamak sağa kaydırılırsa, iki basamaklı boşluk sıfırlarla doldurulduğundan sayı 7.200'e değişir

Adım 4. Ondalık noktayı, paydaki ondalık noktanın hemen yukarısındaki uzun bölme çubuğuna yerleştirin
0,5'i tam sayı yapmak için ondalık basamağı bir basamak kaydırdığınız için, ondalık basamağı bölme çubuğunun üzerine tam olarak ondalık basamağın kaydırıldığı yere, yani 655'teki son 5'ten sonra yerleştirmek iyi bir fikirdir.

Adım 5. Problemi basit uzun bölme ile çözün
655'i 5'e bölmek için adımlar şunlardır:
- Payın (6) yüzler basamağını payda (5) ile bölün. Sonuç 1 ve kalan 1'dir. Bölen çubuğunun üstüne 1 sayısını, çıkarılacak 6 sayısının altına 5 yazın.
- 1'in kalanı, payın (5) onlar basamağından çıkarılır, böylece şimdi 15 elde edersiniz. 15'i 5'e bölerek 3'ü elde edin. Bölen çubuğunun üzerine, 1'in sağına 3 yazın.
- Son 5 haneyi bırakın. 5'i 5'e bölerek 1'i elde edin. Bölen çubuğunun üzerine 3 sayısının sağına 1 sayısını yazın. 5 5'e tam bölünebildiğinden kalan yoktur.
- Uzun ardışık bölme cevabı 655 5 = 131'dir. Bu sonuç 65.5 0,5 sorularının cevabı ile aynıdır.






