Bir matris, satırlar ve sütunlardaki sayıların, sembollerin veya ifadelerin dikdörtgen bir düzenlemesidir. Bir matrisi çarpmak için, matrisin ilk satırındaki öğeleri (veya sayıları) matrisin ikinci satırındaki öğelerle çarpmanız ve çarpımı toplamanız gerekir. Matrisleri, sonuçların doğru eklenmesini, çarpmasını ve yerleştirilmesini gerektiren birkaç kolay adımda çarpabilirsiniz.
Adım
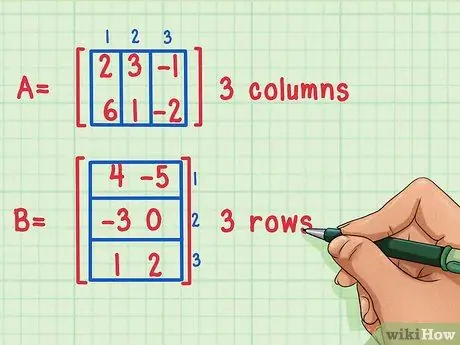
Adım 1. Matrislerin çarpılabilir olduğundan emin olun
Bir matrisi ancak birinci matrisin sütun sayısı ikinci matrisin satır sayısına eşitse çarpabilirsiniz.
Bu matrisler çarpılabilir, çünkü ilk matris, Matrix A'nın 3 sütunu, ikinci matris olan Matrix B'nin ise 3 satırı vardır
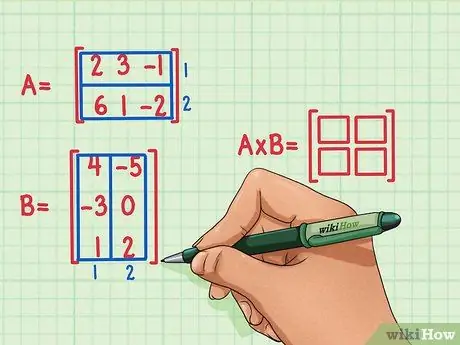
Adım 2. Matris ürününün boyutlarını işaretleyin
İki matrisin çarpımının boyutlarını işaretleyecek yeni, boş bir matris oluşturun. Matris A ve Matris B'nin çarpımını temsil eden matris, birinci matrisle aynı sayıda satıra ve ikinci matrisle aynı sayıda sütuna sahip olacaktır. Bu matristeki satır ve sütun sayısını göstermek için boş kutular çizebilirsiniz.
- Matris A'nın 2 satırı vardır, bu nedenle matrisin çarpılmasının sonucu 2 satır olacaktır.
- Matris B'nin 2 sütunu vardır, bu nedenle matrisin çarpılmasının sonucu 2 sütun olacaktır.
- Matris ürününün sonucu 2 satır ve 2 sütuna sahip olacaktır.
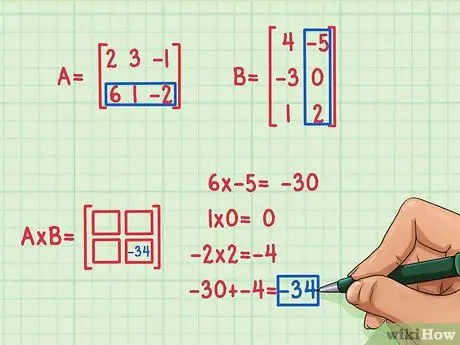
Adım 3. İlk nokta ürününün sonucunu bulun
Birinci nokta çarpımının sonucunu bulmak için, ilk satırdaki ilk öğeyi birinci sütundaki ilk öğeyle, ilk satırdaki ikinci öğeyi birinci sütundaki ikinci öğeyle ve üçüncü öğedeki üçüncü öğeyi çarpmanız gerekir. ilk sütundaki üçüncü öğenin ilk satırı. Ardından, bulmak için çarpma sonuçlarını toplayın. nokta ürün (nokta).
Diyelim ki matris ürününün ilk olarak ikinci satırındaki ve ikinci sütundaki (sağ alt) elemanları hesaplamaya karar verdiniz. İşte bunu nasıl yapacağınız:
- 6 x -5 = -30
- 1 x 0 = 0
- -2x2 = -4
- -30 + 0 + (-4) = -34
-
Nokta çarpım sonucu -34'tür ve bu sonuç matris çarpımının sağ alt köşesine yazılır.
Bir matrisi çarptığınızda, birinci matrisin satır konumuna ve ikinci matrisin sütun konumuna nokta ürün yazılır. Örneğin, Matris A'nın alt satırının ve Matris B'nin sağ sütununun nokta çarpımını biliyorsanız, cevap, -34, matris çarpımının alt satırına ve sağ sütununa yazılır
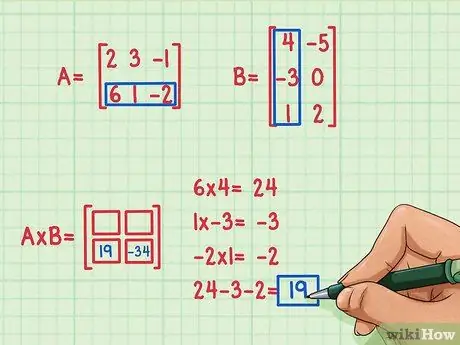
Adım 4. İkinci nokta çarpımının sonucunu bulun
Matris çarpımının sol alt köşesindeki terimi bulmak istediğinizi varsayalım. Bu terimi bulmak için, ilk matrisin alt satırındaki öğeleri ikinci matrisin ilk sütunundaki öğelerle çarpmanız ve ardından toplamanız yeterlidir. İlk satırı ve sütunu çarparken aynı yöntemi kullanın – tekrar bulun nokta çarpım (yapmayın)onun.
- 6 x 4 = 24
- 1 x (-3) = -3
- (-2) x 1 = -2
- 24 + (-3) + (-2) = 19
- Nokta çarpım sonucu -19'dur ve bu sonuç matris çarpımının sol alt kısmına yazılır.
Adım 5. Diğer iki noktalı ürünü bulun
Matris çarpımının sol üst köşesindeki terimi bulmak için, Matris A'nın üst satırının ve Matris B'nin sol sütununun nokta çarpımını bularak başlayın. Bunu şu şekilde yapabilirsiniz:
- 2x4 = 8
- 3 x (-3) = -9
- (-1) x 1 = -1
- 8 + (-9) + (-1) = -2
-
Nokta çarpım sonucu -2'dir ve bu sonuç matris çarpımının sol üst köşesine yazılır.
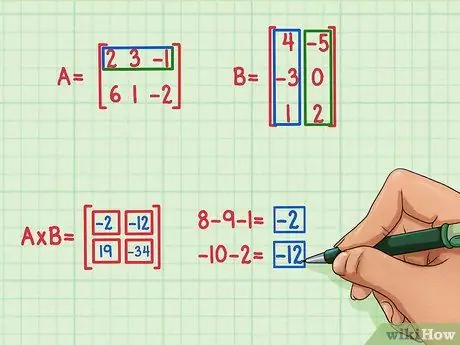
Matris çarpımının sağ üst köşesindeki terimi bulmak için, sadece Matrix A'nın üst satırının ve Matrix B'nin sağ sütununun nokta çarpımını arayın. Bunu nasıl yapacağınız aşağıda açıklanmıştır:
- 2 x (-5) = -10
- 3 x 0 = 0
- (-1) x 2 = -2
- -10 + 0 + (-2) = -12
- Nokta çarpım -12'dir ve bu sonuç matris çarpımının sağ üst köşesine yazılır.
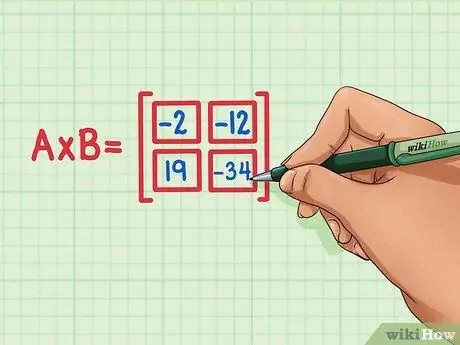
Adım 6. Dört nokta çarpımının matris ürününde doğru yerde olduğundan emin olun
19 sol altta, -34 sağ altta, -2 sol üstte ve -12 sağ üstte olmalıdır.
İpuçları
- Doğru parçalarını kullanmak ve doğruları kullanmamak yanlış cevap verebilir. Bir satırı temsil eden bir çizgi, bir sütunu geçmek için bir uzantı gerektiriyorsa, uzatın! Bu, ürünün her bir öğesiyle çalışmak için hangi satırları ve sütunları kullanacağınızı bilmenizi kolaylaştıran bir görselleştirme tekniğidir.
- İki matrisin çarpımı, birinci matrisin satır sayısına eşit satır sayısını ve ikinci matrisin sütun sayısına eşit sütun sayısını üretecektir.
- Toplamını yaz. Matrisleri çarpmak çok sayıda hesaplama içerir ve yoldan çıkmak ve hangi sayıyı çarptığınızı unutmak çok kolaydır.
