- Yazar Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:25.
- Son düzenleme 2025-06-01 06:08.
P değeri, bilim adamlarının hipotezlerinin doğru olup olmadığını belirlemelerine yardımcı olan istatistiksel bir ölçümdür. P değeri, deneylerinin sonuçlarının, çalışılan şeyler için normal olan değerler aralığında olup olmadığını belirlemek için kullanılır. Genellikle, bir veri kümesinin P değeri önceden belirlenmiş belirli bir değerin (örneğin, 0.05) altına düşerse, bilim adamları deneylerinin sıfır hipotezini reddederler - başka bir deyişle, deneysel değişkenin olduğu bir hipotezi dışlarlar. sonuç üzerinde önemli bir etkisi yok. Günümüzde p değerleri genellikle referans tablolarında ki kare değeri hesaplanarak bulunur.
Adım

Adım 1. Deneyinizin beklenen sonuçlarını belirleyin
Genellikle bilim adamları bir deney yaptıklarında ve sonuçları incelediklerinde, normal veya sıradan sonuçlar hakkında önceden bir fikre sahip olurlar. Bu, önceki deneylerin sonuçlarına, güvenilir gözlemsel veri setlerine, bilimsel literatüre ve/veya diğer kaynaklara dayanabilir. Deneyiniz için, beklediğiniz sonucu belirleyin ve bir sayı olarak yazın.
Örnek: Daha önce yapılan bir araştırmanın, ulusal düzeyde, kırmızı arabalara mavi arabalardan daha sık olarak hız cezası verildiğini gösterdiğini varsayalım. Ulusal düzeydeki ortalama sonucun, kırmızı araba oranı daha fazla olmak üzere 2: 1 oranını gösterdiğini varsayalım. Şehrimizde polis tarafından düzenlenen hız cezasını inceleyerek şehrimizde polisin de aynı eğilime sahip olup olmadığını öğrenmek istiyoruz. Şehrimizde hem kırmızı hem de mavi arabalara verilen 150 hız cezasından rastgele bir örnek alsaydık, 100 kırmızı araba için ve 50 mavi arabalar için ilimizdeki polis birimi ulusal düzeydeki karşılaştırmaya göre bir bilet verirse.

Adım 2. Deneysel gözlemlerinizi belirleyin
Artık beklenen değerinizi belirlediğinize göre, denemenizi çalıştırabilir ve gerçek değeri (veya gözlemi) bulabilirsiniz. Yine, sonucu bir sayı olarak yazın. Bazı deneysel koşulları değiştirirsek ve gözlemlenen sonuçlar beklenen sonuçlardan farklıysa, iki olasılık vardır: ya bu tesadüfen oldu ya da bu farklılığa neden olan deneysel değişkenleri bizim manipülasyonumuzdu. p-değerini bulmanın amacı temel olarak, gözlemlenen sonuçların beklenen sonuçlardan, sıfır hipotezinin (deneysel değişken ile gözlenen sonuçlar arasında hiçbir ilişki olmadığı hipotezinin) reddedilemeyeceği bir noktaya kadar farklı olup olmadığını belirlemektir.
Örnek: Diyelim ki şehrimizde hem kırmızı hem de mavi arabalara verilen 150 hız cezasını rastgele seçtik. alırız 90 kırmızı bir araba için bir bilet ve 60 mavi araba için. Bu, beklediğimiz sonuçtan farklıdır, yani 100 ve 50. Deneysel manipülasyonumuz (bu durumda, veri kaynağını ulusaldan yerele değiştirmek) sonuçlarda herhangi bir değişikliğe neden oldu mu, yoksa şehir polisimiz ulusal düzeyde aynı eğilimlere mi sahipti ve biz sadece tesadüf mü gözlemledik? p değeri onu belirlememize yardımcı olacaktır.

Adım 3. Deneyiniz için serbestlik derecelerini belirleyin
Serbestlik dereceleri, incelediğiniz kategori sayısına göre belirlenen çalışmadaki değişkenlik miktarının bir ölçüsüdür. Serbestlik dereceleri için denklem Serbestlik derecesi = n-1, burada n, denemenizde analiz edilen kategori veya değişkenlerin sayısıdır.
-
Örnek: Deneyimizin iki sonuç kategorisi vardır: biri kırmızı araba için diğeri mavi araba için. Böylece, deneyimizde 2-1 = 1 serbestlik derecesi.
Kırmızı, mavi ve yeşil arabaları karşılaştırırsak, Adım 2. serbestlik derecesi vb.

Adım 4. Ki kare kullanarak beklenen sonuçları gözlemlenen sonuçlarla karşılaştırın
Ki kare (yazılı x2) deneyden beklenen ve gözlenen değerler arasındaki farkı ölçen sayısal bir değerdir. Ki kare denklemi: x2 = ((o-e)2/e), burada o gözlemlenen değerdir ve e beklenen değerdir. Tüm olası sonuçlar için bu denklemin sonuçlarını toplayın (aşağıya bakın).
- Bu denklemin (sigma) operatörünü kullandığını unutmayın. Başka bir deyişle, ((|o-e|-.05) hesaplamanız gerekir.2/e) her olası sonuç için, ki kare değerini elde etmek için sonuçları toplayın. Örneğimizde iki sonucumuz var - kırmızı veya mavi bilet alan bir araba. Böylece ((o-e) hesaplayabiliriz2/e) iki kez - bir kez kırmızı araba için ve bir kez mavi araba için.
-
Örnek: Beklenen değerlerimizi ve gözlemlerimizi x denklemine yerleştirelim2 = ((o-e)2/e). Unutmayın, sigma operatörü nedeniyle ((o-e) hesaplamamız gerekir.2/e) iki kez - bir kez kırmızı araba için ve bir kez mavi araba için. İşlem adımları aşağıdaki gibidir:
- x2 = ((90-100)2/100) + (60-50)2/50)
- x2 = ((-10)2/100) + (10)2/50)
- x2 = (100/100) + (100/50) = 1 + 2 = 3.

Adım 5. Bir önem düzeyi seçin
Artık deneysel kitimizin serbestlik derecelerini ve ki kare değerini bildiğimize göre, p-değerimizi bulmadan önce yapmamız gereken son bir şey var - anlamlılık düzeyini belirlememiz gerekiyor. Temel olarak, anlamlılık düzeyi, sonuçlarımızdan ne kadar emin olduğumuzun bir ölçüsüdür - düşük bir önem düzeyi, bir deneyin sonucunun şansa bağlı olma olasılığının düşük olmasına karşılık gelir ve bunun tersi de geçerlidir. Önem düzeyi, deneyin sonucunun şansa bağlı olma olasılığının yüzdesine (bu durumda %1) karşılık gelen ondalık sayı (örn. 0.01) olarak yazılır.
- Geleneksel olarak, bilim adamları genellikle deneyleri için yüzde 0,05 veya 5 olarak bir anlamlılık değeri belirlerler. Bu, bu anlamlılık düzeyine karşılık gelen deneysel sonuçların en fazla %5 tesadüf şansına sahip olduğu anlamına gelir. Başka bir deyişle, sonuçların bilim insanının deneysel değişkenleri manipüle etmesinden kaynaklanma olasılığı %95'tir ve tesadüf değildir. Çoğu deney için, iki değişken arasındaki ilişki hakkında %95 güvenin, ikisi arasındaki ilişkiyi göstermede başarılı olduğu kabul edilir.
- Örnek: Kırmızı ve mavi araba örneğimiz için bilimsel anlaşmayı takip edelim ve anlamlılık seviyemizi belirleyelim. 0, 05.
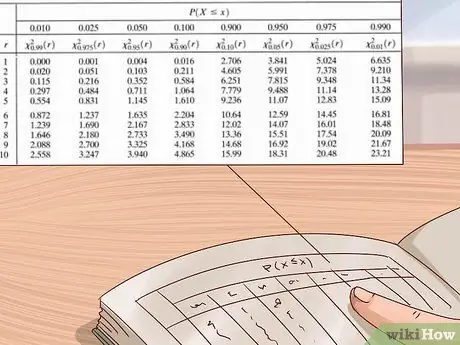
Adım 6. P-değerinizi tahmin etmek için ki kare dağılım tablosunu kullanın
Bilim adamları ve istatistikçiler, deneyleri için p değerlerini hesaplamak için büyük değer tabloları kullanır. Bu tablo genellikle dikey eksen solda serbestlik derecelerini ve yatay eksen üstte p değerlerini gösterecek şekilde yazılır. Bu tabloyu önce serbestlik derecenizi bularak, ardından ki kare değerinizden büyük olan ilk değeri bulana kadar satırları soldan sağa okuyarak kullanın. Sütunun üstündeki p değerine bakın - p değeriniz bu değer ile bir sonraki en büyük değer arasındadır (sağdaki değer onun solundadır).
- Ki-kare dağılım tabloları çeşitli kaynaklardan temin edilebilir - çevrimiçi olarak veya bilim veya istatistik ders kitaplarında kolayca bulunabilirler. Eğer yoksa, yukarıdaki fotoğrafta gösterilen tabloyu veya burada medcalc.org tarafından sağlanan gibi ücretsiz bir çevrimiçi tabloyu kullanın.
-
Örnek: Ki karemiz 3'tür. O halde, yaklaşık bir p-değeri bulmak için yukarıdaki fotoğraftaki ki kare dağılım tablosunu kullanalım. Deneyimizin yalnızca
Aşama 1. serbestlik dereceleri, üst tablodan başlayacağız. Daha yüksek bir değer bulana kadar bu satırda soldan sağa gideriz.
Aşama 3. - ki kare değerimiz. Bulduğumuz ilk değer 3.84'tür. Bu sütuna baktığımızda, karşılık gelen p-değerinin 0.05 olduğunu görüyoruz. Bu, p-değerimizin olduğu anlamına gelir. 0,05 ile 0,1 arasında (tablodaki bir sonraki en büyük p değeri).

Adım 7. Boş hipotezinizi reddetmeye veya savunmaya karar verin
Denemeniz için yaklaşık bir p-değeri bulduğunuz için, denemenizin boş hipotezini reddedip reddetmemeye karar verebilirsiniz (hatırlatmak gerekirse, bu, manipüle ettiğiniz deneysel değişkenin gözlemlediğiniz sonuçlar üzerinde hiçbir etkisi olmadığı hipotezidir). Eğer p değeriniz anlamlılık değerinizden düşükse tebrikler - manipüle ettiğiniz değişkenler ile gözlemleriniz arasında bir ilişki olma olasılığının yüksek olduğunu kanıtladınız. Eğer p değeriniz anlamlılık değerinizden büyükse, gözlemlediğiniz sonuçların yalnızca tesadüfün veya denemenizin manipülasyonunun sonucu olduğunu kesin olarak söyleyemezsiniz.
- Örnek: p-değerimiz 0,05 ile 0,1 arasındadır. Yani, hiçbir şekilde 0,05'ten küçük değildir, bu nedenle ne yazık ki, biz sıfır hipotezimizi reddedemez. Bu da şehrimizde polisin kırmızı ve mavi arabalara ulusal ortalamadan oldukça farklı bir oranda bilet verdiğini söyleyebilmek için belirlediğimiz minimum %95 güven sınırına ulaşamıyoruz demektir.
- Başka bir deyişle, gözlemlerimizin bir yer değişikliğinin (şehrimizin tamamını değil, tamamını değil) bir sonucu olmadığını, tesadüfi olma ihtimali %5-10'dur. %5'ten daha az bir olasılık aradığımızdan, bunu yaptığımızı söyleyemeyiz. ikna edilmiş şehrimizdeki polisin kırmızı arabaları cezalandırma eğiliminde olduğunu - bu eğilime sahip olmamalarına dair hafif ama istatistiksel olarak çok farklı bir olasılık var.
İpuçları
- Bilimsel bir hesap makinesi hesaplamaları çok daha kolay hale getirecektir. Ayrıca çevrimiçi hesaplayıcıları da arayabilirsiniz.
- Yaygın olarak kullanılan elektronik tablo yazılımı ve daha özel istatistiksel yazılımlar dahil olmak üzere çeşitli bilgisayar programlarını kullanarak p-değerlerini hesaplayabilirsiniz.






