İstatistikte, aralık, bir veri kümesindeki en yüksek değer ile bir veri kümesindeki en düşük değer arasındaki farktır. Aralık, değerlerin bir dizide ne kadar yayıldığını gösterir. Aralık büyük bir sayıysa, dizideki değerler oldukça dağınıktır; aralık küçük bir sayı ise serideki değerler birbirine yakındır. Erişimi nasıl hesaplayacağınızı öğrenmek istiyorsanız, aşağıdaki adımları uygulamanız yeterlidir.
Adım
Adım 1. Veri kümenizin öğelerini listeleyin
Bir veri kümesinin aralığını bulmak için, en büyük ve en küçük sayıları tanımlayabilmeniz için veri kümesindeki tüm öğeleri listelemelisiniz. Tüm unsurları yazın. Bu veri setindeki sayılar: 14, 19, 20, 24, 25 ve 28.
- Sayıları küçükten büyüğe sıralarsanız, bir veri kümesindeki en büyük ve en küçük sayıları belirlemek daha kolaydır. Bu örnekte, veri seti şu şekilde yapılandırılacaktır: 14, 19, 20, 24, 24, 25, 28.
- Bir veri kümesindeki öğeleri sıralamak, veri kümesinin modunu, ortalamasını veya medyanını bulmak gibi diğer hesaplamaları yapmanıza da yardımcı olacaktır.
Adım 2. Veri kümesindeki en büyük ve en küçük sayıları belirleyin
Bu problemde veri setindeki en küçük sayı 14, en büyük sayı 28'dir.
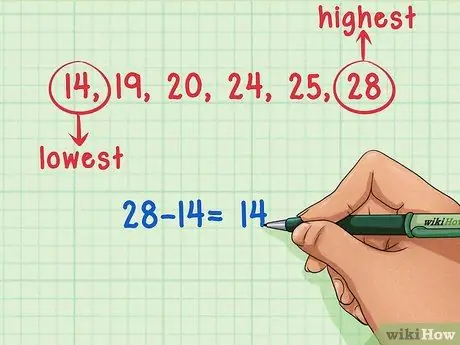
Adım 3. Veri kümenizdeki en küçük sayıyı en büyük sayıdan çıkarın
Artık veri kümesindeki en küçük ve en büyük sayıları belirlediğinize göre, tek yapmanız gereken bunları birbirinden çıkarmak. Veri kümesinin aralığı olan 11'i elde etmek için 25'ten (25 – 14) 14 çıkarın.
Adım 4. Aralığı net bir şekilde etiketleyin
Aralığı bulduğunuzda, açıkça etiketleyin. Bu, medyan, mod veya ortalamayı bulmak gibi gerçekleştirmeniz gerekebilecek diğer istatistiksel hesaplamalarla karışıklığı önlemenize yardımcı olacaktır.
İpuçları
- Aralığı cebirsel terimlerle de yorumlayabilirsiniz, ancak önce cebirsel bir işlev kavramını veya bilinen sayılar üzerindeki bir dizi işlemi anlamalısınız. Fonksiyon işlemleri herhangi bir sayı üzerinde, hatta bilinmeyen bir sayı üzerinde gerçekleştirilebildiğinden, sayı, genellikle x olan bir harf değişkeni ile gösterilir. Etki alanı, bilinmeyen sayının yerine kullanabileceğiniz bir dizi olası giriş değeridir. Bu nedenle, aralık, etki alanı değerlerinden birini girdikten ve fonksiyon tarafından tanımlanan tüm işlemleri tamamladıktan sonra elde ettiğiniz olası hesaplama sonuçları kümesidir. Ne yazık ki, bir fonksiyonun aralığını hesaplamanın bir yolu yoktur. Bazen bir fonksiyonun grafiğini çizmek veya birden çok değeri hesaplamak net bir model gösterebilir. Olası çıktı (hesaplama sonuçları) değerlerini atmak veya aralığı temsil eden veri kümesini daraltmak için işlevin etki alanı hakkındaki bilginizi de kullanabilirsiniz.
- Herhangi bir istatistiksel veri setinin medyan değeri, aralık değil, veri dağılımı açısından veri setinin medyan değerini temsil eder. Bu nedenle, belirli bir veri kümesinin medyanının, aralığın 2'ye bölündüğünü veya aralığın aralığının yarısı olduğunu varsaymak isteyebilirsiniz, ancak bu genellikle doğru değildir. Doğru medyanı bulmak için veri öğelerini sıralamanız ve ardından öğeyi listenin ortasında aramanız gerekir. Bu eleman medyandır. Örneğin, 29 öğeden oluşan bir listeniz varsa, 15. öğe, listenin başından ve listenin sonundan itibaren aynı aralığa sahiptir, bu nedenle, 15. öğe, o öğenin değerinin nasıl ilişkili olduğuna bakılmaksızın medyandır. menzil.
