- Yazar Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:44.
- Son düzenleme 2025-06-01 06:08.
Ondalık (on tabanlı) sayı sistemi, her sayı konumu için on olası değere (0, 1, 2, 3, 4, 5, 6, 7, 8 veya 9) sahiptir. Buna karşılık, ikili (taban iki) sayı sistemi, her sayı konumu için 0 ve 1 ile temsil edilen yalnızca iki olası değere sahiptir. İkili sayı sistemi elektronik bilgisayarların iç dili olduğundan, ciddi bilgisayar programcıları ondalık sayı sisteminden ikili sayı sistemine nasıl dönüştürüleceğini bilirler. Bu kolay adımları ve ayrıca bu dönüşümde nasıl ustalaşacağınızı izleyin.
Adım
Yöntem 1/2: Kalan ile İkiye Kısa Bölme

Adım 1. Sorunu belirleyin
Bu örnek için, ondalık sayı 156'yı dönüştürelim10 ikili sayı olsun. Ondalık sayıyı, ters çevrilmiş bölme sembolüne bölünecek sayı olarak yazın. Hedef sayı sisteminin tabanını (bu örnekte ikili için “2”) bölme sembolünün eğri dışı böleni olarak yazın.
- Bu yöntem kağıda çizildiğinde anlaşılması çok daha kolaydır ve yeni başlayanlar için çok daha kolaydır, çünkü yalnızca ikiye böler.
- Dönüştürmeden önce ve sonra karışıklığı önlemek için, her sayı için hesapladığınız sayı sisteminin taban numarasını bir alt simge olarak (ayırıcı işaret olarak normal harflerle küçük harfle yazılır) yazın. Bu örnekte, ondalık sayının alt indisi 10 olacak ve ikili sayının alt indisi 2 olacaktır.

Adım 2. Bölmeyi yapın
Tamsayı cevabını (bölüm) uzun bölme sembolünün altına yazın ve kalanı (0 veya 1) bölünen sayının sağına yazın.
İkiye böldüğümüz için bölünen sayı çift ise kalan 0, bölünen sayı tek ise kalan 1 olur

Adım 3. Sıfıra ulaşana kadar bölmeye devam edin
Her yeni bölümü ikiye bölerek ve kalanını her bölünen sayının sağına yazarak yokuş aşağı devam edin. Bölüm sıfır olduğunda dur.

Adım 4. Yeni ikili sayıyı yazın
Kalan en düşük sayıdan başlayarak, kalanın sırasını artan düzende en üste doğru okuyun. Bu örnekte, 10011100 sonucunu almalısınız. Bu, 156 ondalık sayısının ikili eşdeğeridir. Veya, sayısal taban alt indisi ile yazılmışsa: 15610 = 100111002.
Bu yöntem, ondalık tabandan herhangi bir sayı tabanına dönüştürmek için değiştirilebilir. Bölen 2'dir çünkü hedef sayı sisteminin tabanı 2 tabanıdır (ikili). Hedef sayı sisteminin tabanı başka bir taban ise, bu yöntemdeki taban 2 numarasını uygun taban numarasıyla değiştirin. Örneğin, hedef taban 9 ise, taban 2 sayısını 9 ile değiştirin. Nihai sonuç doğrudan hedef taban numarası şeklinde olacaktır
Yöntem 2/2: İkinin Gücünü Türetme ve Çıkarma

Adım 1. Bir tablo oluşturarak başlayın
"Tablo 2 tabanı"ndaki iki temel sayının güçlerini sağdan sola yazın. 2'de başla0, “1” olarak yazın. Her rütbe için rütbeyi 1 yükseltin. Hesapladığınız ondalık sayı sisteminin sayısına en yakın sayıyı elde edene kadar tabloyu tamamlayın. Bu örnek için, ondalık sayı 156'yı dönüştürelim10 ikili sayı olsun.

Adım 2. Taban sayısı 2'nin en büyük gücüne sahip sayıyı bulun
Tablodan dönüştürülecek sayıya eşit veya ondan küçük olan en büyük sayıyı seçin. 128 sayısı, 2 taban sayısının en büyük kuvvetine sahip sayıdır ve ayrıca 156'dan küçüktür, bu nedenle tablodaki en büyük sayının solda olduğu tabloda bu kutunun altına "1" sayısını yazın (tabloya bakınız). yukarıdaki resimde). Ardından ilk sayıdan 128 çıkarın, şunu elde edeceksiniz: 156 - 128 = 28.
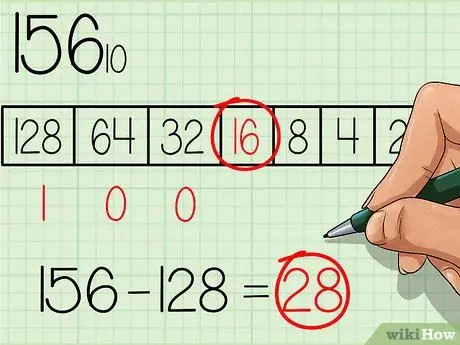
Adım 3. Tablodaki bir sonraki daha küçük güce geçin
Yeni numarayı (28) kullanarak, sayıların yeni numaraya eşit veya küçük olup olmadığını kontrol ederek tabloyu soldan sağa doğru devam ettirin. 64 sayısı 28'den küçük değildir, bu nedenle 64 numaralı kutunun altına "0" sayısını yazın. 28'e eşit veya daha küçük bir sayı bulana kadar devam edin.
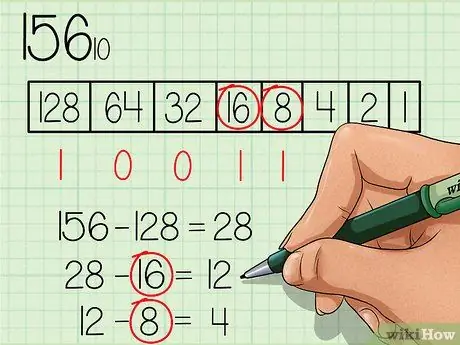
Adım 4. Yeni sayıya eşit veya ondan küçük olan her sayıyı sürekli olarak çıkarın ve uygun sayı için kutunun altındaki “1” sayısını işaretleyin
16 sayısı 28'den küçüktür, bu nedenle 16 numaralı kutunun altına "1" yazın ve 28'den 16 çıkarın, böylece yeni bir 12 sayısı elde edersiniz. 8 sayısı 12'den küçüktür, bu nedenle altına "1" yazın 8 numaralı kutuyu seçin ve yeni 4 sayısını elde etmek için 12'den 8 çıkarın.

Adım 5. Tablonun sonuna ulaşana kadar devam edin
Yeni sayıya eşit veya ondan küçük sayılar için her kutunun altına “1” ve yeni sayıdan hala büyük olan sayılar için her kutunun altına “0” işaretlemeyi unutmayın.
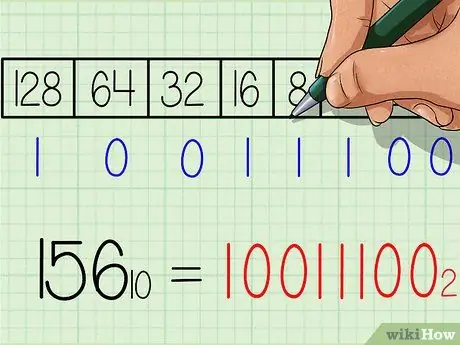
Adım 6. İkili sayının cevabını yazın
Sayı, tablonun altındaki “1” ve “0” sayılarının satırı ile soldan sağa tam olarak aynı olacaktır. 10011100 sonucunu almalısınız. Bu, 156 ondalık sayısının ikili eşdeğeridir. Veya bir alt simge ile yazıldığında: 15610 = 100111002.
Bu yöntemi tekrarlamak, iki tabanın güçlerini hatırlamanıza yardımcı olabilir, böylece 1. adımı atlayabilirsiniz
İpuçları
- İşletim sisteminde yerleşik olarak bulunan Hesap Makinesi programı bu dönüştürmeyi sizin için yapabilir, ancak bir programcı olarak, dönüştürmelerin nasıl çalıştığını iyi bir şekilde anlamakla başlamak en iyisidir. Hesap Makinesi programındaki dönüştürme seçenekleri, “Görünüm” menüsü açılıp “Programcı” seçilerek (Windows 7 ve 8 için) görünür hale getirilebilir.
- Ters yönde, yani ikili sayı sisteminden ondalık sayı sistemine dönüştürme, genellikle ilk önce öğrenmesi daha kolaydır.
- Daha uzman olmak için genellikle ondalık sayıları ikiliye dönüştürme alıştırması yapın.






