- Yazar Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-16 20:04.
- Son düzenleme 2025-01-23 12:50.
Optik aletleri incelerken, mercek benzeri bir nesnenin "büyütmesi", gördüğünüz görüntünün yüksekliğinin nesnenin gerçek yüksekliğine oranıdır. Örneğin, bir nesneyi çok büyük gösterebilen bir mercek "yüksek" bir büyütme faktörüne sahipken, bir nesneyi küçük gösteren bir mercek "düşük" bir büyütme faktörüne sahiptir. Bir nesneyi büyütme formülü genellikle aşağıdaki formül kullanılarak hesaplanır: M = (sben/HÖ) = -(dben/NSÖ), burada M = büyütme, hben = görüntünün yüksekliği, hÖ = nesnenin yüksekliği ve dben ve DÖ = görüntü ve nesnenin mesafesi.
Adım
Yöntem 1/2: Tek Lensli Büyütmenin Hesaplanması
Notlar: Bir Yakınsayan mercek merkezde kenarlardan daha geniş (büyüteç gibi). a ıraksak mercek kenarlarda merkezden daha geniş (bir kase gibi). Her iki lenste de büyütmenin hesaplanması aynıdır. önemli bir istisna. Farklı lenslerdeki istisnalara doğrudan gitmek için buraya tıklayın.
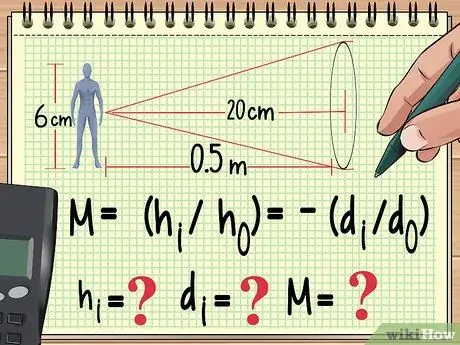
Adım 1. Denkleminiz ve zaten bildiğiniz değişkenlerle başlayın
Herhangi bir fizik probleminde olduğu gibi, bir genişleme problemini çözmenin yolu, onu hesaplamak için kullanacağınız denklemi yazmaktır. Buradan, kullandığınız denklemden bulamadığınız değişkenin değerini bulmak için geriye doğru çalışabilirsiniz.
-
Örneğin, 6 cm boyunda bir oyuncak bebeğin bir metre uzağa yerleştirildiğini varsayalım. Yakınsayan mercek 20 cm odak uzaklığı ile. Büyütme, görüntü yüksekliği ve görüntü mesafesini hesaplamak istiyorsak denklemimizi aşağıdaki gibi yazmaya başlayabiliriz:
-
- M = (sben/HÖ) = -(dben/NSÖ)
-
- Şimdi biliyoruz hÖ (bebeğin yüksekliği) ve dÖ (objektiften bebek mesafesi). Bu denklemde olmayan merceğin odak uzaklığını da biliyoruz. sayacağız Hben, NSben, ve M.

Adım 2. d'yi elde etmek için lens denklemini kullanmaben.
Büyüttüğünüz cisme olan uzaklığı ve merceğin odak uzunluğunu biliyorsanız, oluşan görüntüden uzaklığı hesaplamak mercek denklemi ile çok kolaydır. Lensin denklemi 1/f = 1/dÖ + 1/günben, burada f = merceğin odak uzaklığı.
-
Bu örnek problemde, d'yi hesaplamak için lens denklemini kullanabiliriz.ben. f ve d değerlerini girinben sonra denklemi çözün:
-
- 1/f = 1/dÖ + 1/günben
- 1/20 = 1/50 + 1/dben
- 5/100 - 2/100 = 1/dben
- 3/100 = 1/günben
- 100/3 = dben = 33,3 cm
-
- Merceğin odak uzaklığı, merceğin merkezinden, odak noktasında ışığın iletildiği noktaya olan mesafedir. Bir büyüteçle ışığı yanan karıncalara odakladıysanız, bunu görmüşsünüzdür. Dersteki sorularda genellikle bu sıcak noktanın büyüklüğü verilmiştir. Gerçek hayatta, bu özellikler genellikle lens üzerinde bulunan bir etikete yazılır.

Adım 3. h hesaplanmasıben.
d'yi hesapladıktan sonraÖ ve Dben, büyütülen nesnenin yüksekliğini ve merceğin büyütmesini hesaplayabilirsiniz. Mercek büyütme denklemindeki (M = (h) iki eşittir işaretine dikkat edin.ben/HÖ) = -(dben/NSÖ)) - bu, bu denklemin tüm bölümlerinin birbirine eşit olduğu anlamına gelir, böylece M ve h'yi hesaplayabilirizben istediğimiz sırayla.
-
Bu örnek problem için h'yi hesaplayabiliriz.ben bunun gibi:
-
- (Hben/HÖ) = -(dben/NSÖ)
- (Hben/6) = -(33, 3/50)
- Hben = -(33, 3/50) x 6
- Hben = - 3, 996 cm
-
- Buradaki nesnenin yüksekliğinin negatif olduğuna dikkat edin, bu daha sonra göreceğimiz görüntünün ters çevrileceğini (üst-alt) gösterir.

Adım 4. M'nin Hesaplanması
Son değişkeni -(d) denklemiyle hesaplayabilirsiniz.ben/NSÖ) veya (hben/HÖ).
-
Aşağıdaki örnekte, M'nin nasıl hesaplanacağı aşağıdaki gibidir:
-
- M = (sben/HÖ)
-
M = (-3, 996/6) = - 0, 666
-
-
Sonuç, d değeri kullanılarak hesaplandığında da aynı olacaktır:
-
- M = -(dben/NSÖ)
- M = -(33, 3/50) = - 0, 666
-
- Yakınlaştırmanın bir birim etiketine sahip olmadığını unutmayın.
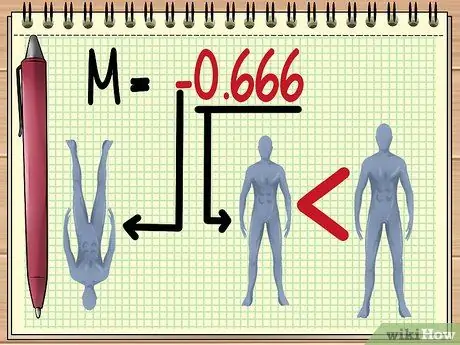
Adım 5. M değerini anlama
M değerinin büyüklüğünü elde ettiğinizde, mercekten göreceğiniz görüntü hakkında birkaç şeyi tahmin edebilirsiniz, yani:
-
Boyut.
M'nin "mutlak değeri" ne kadar büyük olursa, mercekle görüntülenen nesne o kadar büyük görünür. 0 ile 1 arasındaki M değeri, nesnenin daha küçük görüneceğini belirtir.
-
Nesne yönelimi.
Negatif bir değer, oluşturulan görüntünün tersine çevrileceğini gösterir.
- Burada verilen örnekte -0.666 M değeri, mevcut değişkenin değerine göre bebeğin gölgesinin görüneceği anlamına gelir. baş aşağı ve gerçek boyuttan üçte iki daha küçük.
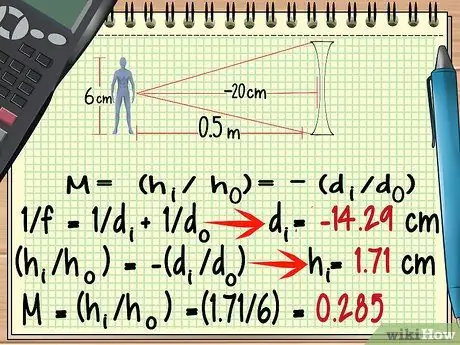
Adım 6. Uzaklaşan bir mercek için negatif bir odak noktası kullanın
Uzaklaşan bir merceğin şekli, yakınsak bir merceğinkinden çok farklı olsa da, büyütme oranını yukarıdakiyle aynı formülü kullanarak hesaplayabilirsiniz. Akılda tutulması gereken istisnalar Uzaklaşan merceğin odak noktası negatiftir.
Yukarıdaki örnek problemde bu, d hesaplamasında alacağınız cevabı etkileyecektir.ben, bu yüzden buna dikkat ettiğinizden emin olun.
-
Yukarıdaki örnek problemi yeniden ele alalım, ancak şimdi odak uzaklığına sahip bir ıraksayan mercek kullanıyoruz - 20 santimetre.
Diğer değişkenler aynı değerde kalır.
-
Her şeyden önce, d'yi hesaplayacağızben lens denklemini kullanarak:
-
- 1/f = 1/dÖ + 1/günben
- 1/-20 = 1/50 + 1/dben
- -5/100 - 2/100 = 1/dben
- -7/100 = 1/günben
- -100/7 = günben = - 14, 29 cm
-
-
Şimdi h hesaplayacağızben ve d değeri olan Mben yeni olan.
-
- (Hben/HÖ) = -(dben/NSÖ)
- (Hben/6) = -(-14, 29/50)
- Hben = -(-14, 29/50) x 6
- Hben = 1, 71 cm
- M = (sben/HÖ)
- M = (1, 71/6) = 0, 285
-
Yöntem 2/2: Çoklu Lenslerin Büyütmesini Hesaplama
Basit İki Lens Yöntemi
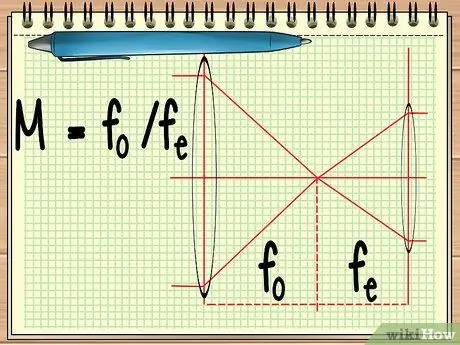
Adım 1. İki merceğin odak noktasını hesaplayın
Yan yana dizilmiş iki mercekten oluşan bir alet (teleskop veya bir çift dürbün gibi) kullandığınızda, iki merceğin genel büyütmesini hesaplamak için tek yapmanız gereken iki merceğin odak noktasını bulmaktır. bu, M = f basit denklemi ile hesaplanabilir.Ö/Fe.
denklemde, fÖ objektif merceğin odak noktasıdır ve fe göz merceğinin odak noktasıdır. Objektif lens, nesneye yakın olan büyük lenstir, oküler lens ise gözlemcinin gözüne yakın bulunan lenstir.

Adım 2. Zaten sahip olduğunuz bilgiyi M = f denklemine ekleyinÖ/Fe.
Her iki merceğin odak noktalarına sahip olduğunuzda, bunları hesaplamak çok kolaydır, - Objektif merceğin odak uzaklığını okülerin odak uzaklığına bölerek oranı hesaplayın. Aldığınız cevap, aracın toplam büyütmesidir.
-
Örneğin, basit bir teleskop varsayalım, objektif merceğin odak noktasının 10 cm ve göz merceğinin odak noktasının 5 cm olduğu yazıldığında, büyütme 10/5 = 2.
Karmaşık Yöntem
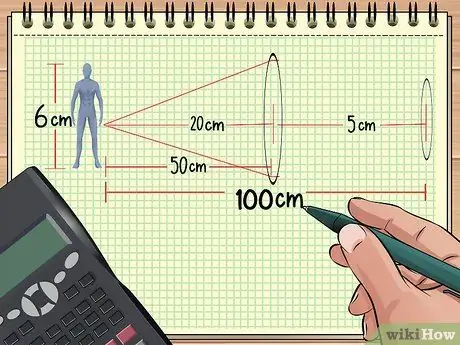
Adım 1. Lensler ve nesne arasındaki mesafeyi hesaplayın
Bir nesnenin önünde arka arkaya düzenlenmiş iki lensiniz varsa, lenslerden nesneye olan mesafeyi, nesnenin boyutunu ve iki lensin odak noktasını biliyorsanız, toplam büyütme hesaplanabilir. Kalan kısım da hesaplanabilir.
Örneğin, yukarıdaki örnek problem 1'deki gibi nesneleri ve lensleri düzenlediğimizi varsayalım: bir oyuncak bebek, odak uzunluğu 20 cm olan yakınsak bir mercekten 50 cm uzaktadır. Şimdi odak noktalı ikinci merceği ilk mercekten (bebekten 100 cm) 50 cm uzağa 5 cm uzağa yerleştirin. Bundan sonra elde ettiğimiz bilgileri kullanarak toplam büyütmeyi hesaplayacağız
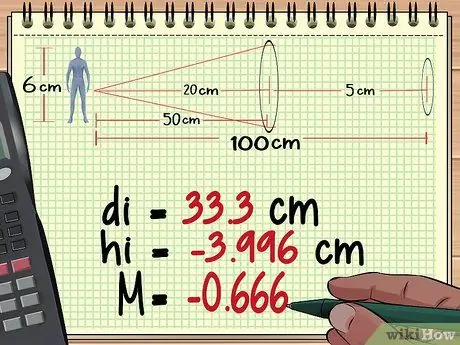
Adım 2. Objektif 1'den nesne mesafesini, yüksekliğini ve büyütmesini hesaplayın
Birden fazla merceğin büyütmesini hesaplamanın ilk kısmı, tek bir merceğin büyütmesini hesaplamakla aynıdır. Nesneye en yakın mercekle başlayın, oluşan görüntüden uzaklığı bulmak için mercek denklemini kullanın, ardından görüntünün yüksekliğini ve büyütmesini bulmak için büyütme denklemini kullanın. Daha fazla tek lens büyütme hesaplamasını görmek için buraya tıklayın.
-
Yukarıdaki Yöntem 1'deki hesaplamalarımızdan, ilk merceğin şu kadar yüksek bir görüntü ürettiğini bulduk. - 3, 996 cm, mesafe 33,3 cm merceğin arkasında ve büyütmede - 0, 666.
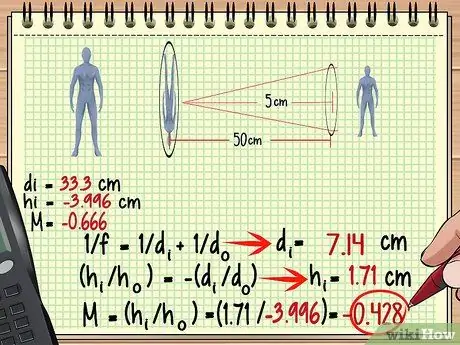
Adım 3. Birinci mercekteki görüntüyü ikinci mercekteki nesne olarak kullanın
Şimdi, ikinci mercek için büyütme, yükseklik ve daha fazlasını bulmak çok kolay - sadece ilk mercek için kullandığınız yöntemi kullanın, yalnızca bu sefer görüntüyü bir nesne olarak ele alın. İkinci merceğe olan görüntü mesafesinin her zaman ilk merceğe olan nesne mesafesiyle aynı olmadığını unutmayın.
-
Yukarıdaki örnekte görüntü ilk merceğin 33,3 cm arkasında oluştuğu için mesafe 50-33.3 = 16,7 cm ikinci lensin önünde. İkinci merceğin oluşturduğu görüntüyü bulmak için bu ölçümü ve ikinci merceğin odak uzunluğunu kullanalım.
-
- 1/f = 1/dÖ + 1/günben
- 1/5 = 1/16, 7 + 1/dben
- 0, 2 - 0, 0599 = 1/dben
- 0, 14 = 1/günben
- NSben = 7, 14 cm
-
-
Şimdi h'yi hesaplayabilirizben ve ikinci lens için M:
-
- (Hben/HÖ) = -(dben/NSÖ)
- (Hben/-3, 996) = -(7, 14/16, 7)
- Hben = -(0, 427) x -3, 996
- Hben = 1, 71 cm
- M = (sben/HÖ)
- M = (1, 71/-3, 996) = - 0, 428
-
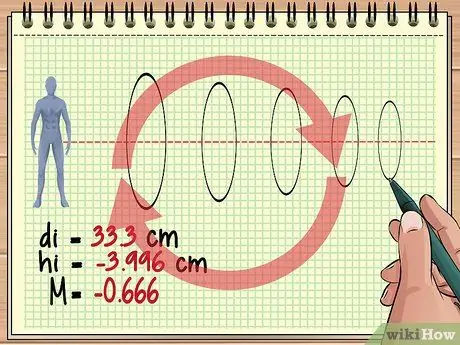
Adım 4. Ek lensler için bu şekilde hesaplamaya devam edin
Bu temel yaklaşım, bir nesnenin önünde sıralanmış üç, dört veya yüzlerce mercek varsa aynıdır. Her mercek için, önceki merceğin görüntüsünü nesne olarak kabul edin ve istediğiniz yanıtı bulmak için mercek denklemini ve büyütme denklemini kullanın.
Her bir sonraki merceğin oluşan görüntüyü sürekli olarak tersine çevirebileceğini unutmayın. Örneğin, daha önce elde ettiğimiz büyütme değeri (-0, 428) göreceğimiz görüntünün gerçek nesne boyutunun yaklaşık 4/10'u olduğunu, ancak önceki mercekten gelen görüntü ters olduğu için dik olduğunu gösterir
İpuçları
- Dürbünler genellikle büyütme özelliklerinin bir açıklamasını başka bir sayının çarpımı şeklinde sağlar. Örneğin dürbün 8x25 veya 8x40 olarak belirtilebilir. Böyle yazıldığında, ilk sayı dürbünün büyütmesidir. Verilen örnekte iki sayının büyüklükleri farklı olsa bile, her iki dürbün de 8 kat büyütmeli. İkinci sayı, görüntünün dürbün tarafından ne kadar net oluşturulacağını gösterir.
- Tek mercekli büyüteç için, nesne mesafesi merceğin odak uzunluğundan büyükse büyütmenin negatif olacağını unutmayın. Bu, oluşan görüntünün daha küçük olacağı anlamına gelmez. Bu durumda, büyütme devam eder, ancak oluşan görüntü gözlemci tarafından baş aşağı (yukarıdan aşağıya) görülecektir.






